One of my fellow researchers asked me this question, which he said was an interview question for amazon.

Write an algorithm to reverse blocks of length k- in a list. i.e. if k=3 and the list is originally ; it should produce .

There’s already a clever trick to reverse a linked list without requiring any extra space. The idea is that we just iterate through the list and reverse all the pointers. In java this would look something like this

	public static Node reverse(Node list){
		Node prev = null;
		while(list != null){
			Node next = list.next;
			list.next = prev;
			prev = list;
			list = next;
		}
		return prev;
	}

This will reverse the entire list (by going until the next link is null), so if we want to reverse blocks of length 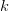instead, we should add an additional parameter and condition, to obtain below.

	public static Node reverse(Node list, int k){
		Node prev = null;
		while(list != null && k-- > 0){
			Node next = list.next;
			list.next = prev;
			prev = list;
			list = next;
		}
		return prev;
	}

So what happens when we call reverse on a list? Imagine we have the list 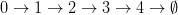after a call to reverse with 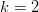on the first node (0), the list will be , and the call returns a pointer to ‘1’. Now we see that the trick we need to overcome is losing our place in the list as we do the block-wise reversal. I did this by keeping track of basically three positions : the first element of the block you are going to reverse, the last element of this block (which is returned by the call to reverse) and the first element of the next block to be reversed.

This way, after we have reversed the first j-1 blocks, we only need to reverse block j, point the end of block j-1 to the new beginning of block j, and then update positions to go to block j+1. In code this looks like… (I handle the first block specially so we know how to return the start of the list)

	public static Node kreverse(Node list, int k){
		Node prev = list;
		int i = 0;

		//first block special case?
		while(list != null && i++ < k){
			list = list.next;
		}
		Node retval = reverse(prev, k);

		while(list != null){
			i = 0;
			Node me = list;
			while(list != null && i++ < k)
				list = list.next;
			Node end = reverse(me, k);
			prev.next = end;

			prev = me;
		}

		return retval;
	}

What is great is that we have only visited each element in the list about twice, (once in the inner while loop of kreverse, and once in reverse) and at most constant extra space. In fact, we can even avoid visiting each element twice if we are clever with the reverse method, and return multiple values (Python!!!!). So this method is 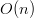in both time and complexity. One other consideration is what will happen if the length of the list is not divisible by .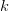